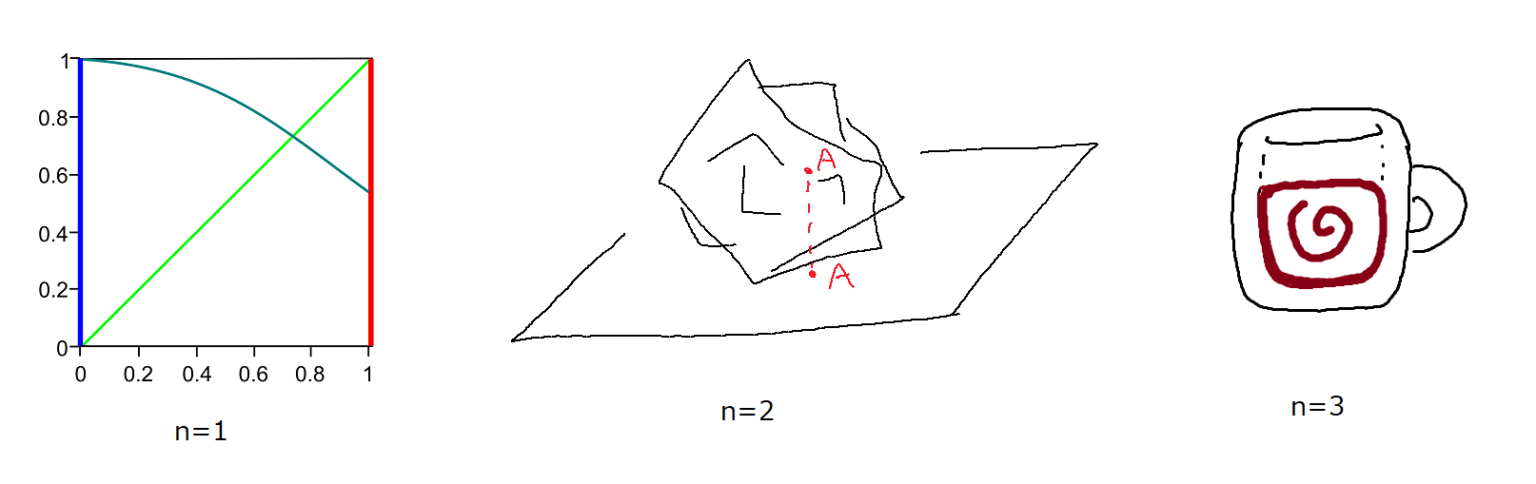
ブラウワーの不動点定理

ブラウワーの不動点定理（ブラウワーのふどうてんていり、英: Brouwer's fixed-point theorem）は、位相幾何学における不動点定理で、ライツェン・ブラウワーの名にちなむ。この定理では、コンパクト凸集合からそれ自身への任意の連続函数 f に対して、f(x₀) = x₀ を満たす点 x₀、すなわち不動点が存在することが述べられている。ブラウワーの定理の最も簡単な形式のものは、実数直線内の閉区間 I あるいは閉円板 D からそれ自身への連続函数 f に対するものである。後者に対するより一般のものは、ユークリッド空間の凸コンパクト部分集合 K からそれ自身への連続函数に対するものである。

不動点定理は数多く存在するが、中でもブラウワーの不動点定理は数学の多くの分野をまたいで利用されるため、非常に有名である。元々の分野において、この結果はジョルダン曲線定理、毛球の定理およびボルサック＝ウラムの定理とともにユークリッド空間のトポロジーを特徴付ける重要な定理となっている。このため、この定理は位相幾何学における基礎的な定理に位置付けられている。この定理はまた、微分方程式の重要な結果を証明するために用いられ、微分幾何学の入門的なほとんどの課程において扱われている。この定理はまた、ゲーム理論のような分野でも用いられている。経済学において、ブラウワーの不動点定理とその拡張である角谷の不動点定理は、1950年代にノーベル経済学賞受賞者のケネス・アローとジェラール・ドブルーによって示されたように、マーケット経済の一般均衡の存在の証明で中心的な役割を果たしている。 さらに数値解析の分野においては、非線型方程式の数値解に対する精度保証付き数値計算の基礎として利用される。

この定理ははじめ、アンリ・ポアンカレとエミール・ピカールを中心とするフランスの数学者によって微分方程式の観点から研究されていた。ポアンカレ＝ベンディクソンの定理のような結果を証明する上で、位相幾何学的な手法を利用することが求められていた。19世紀末においてこの研究は、いくつかの定理を証明するに至った。一般的な場合は1910年にジャック・アダマールとライツェン・ブラウワーによって証明された。

内容

この定理には、使用される文脈と一般化の程度に応じて、いくつかの異なるヴァージョンがある。最も簡単なものは次である：

平面における定理

閉円板からそれ自身へのすべての連続函数は少なくとも一つの不動点を持つ。

これは任意の有限次元空間に対して次のように一般化される：

ユークリッド空間における定理

ユークリッド空間の閉球からそれ自身へのすべての連続函数は不動点を持つ。

より一般的な場合は次である：

コンパクト凸集合における定理

ユークリッド空間のコンパクト凸部分集合 K からそれ自身へのすべての連続函数は不動点を持つ。

より一般的な場合は、次のような異なる名前で知られている：

シャウダーの不動点定理

バナッハ空間のコンパクト凸部分集合 K からそれ自身へのすべての連続函数は不動点を持つ。

各条件の重要性

この定理は、コンパクト、すなわち「有界」かつ「閉」で、さらに「凸」である集合に対してのみ成立する。次の例は、これら三つの条件がなぜ重要なのかという点を示すものである。

有界性

R からそれ自身への連続函数

${\displaystyle f(x)=x 1}$

を考える。この函数はすべての点を右側に写すため、不動点を持つことはない。R は凸かつ閉であるが、有界でないことに注意されたい。

閉性

開区間 (−1,1) からそれ自身への連続函数

${\displaystyle f(x)={\frac {x 1}{2}}}$

を考える。この区間において、この函数はすべての点を右側に写すため、不動点を持つことはない。(−1,1) は凸かつ有界であるが、閉でないことに注意されたい。しかし閉区間 [−1,1] 上では、この函数 f は不動点を持つ。f(x) = x = 1。

凸性

凸性は、ブラウワーの不動点定理において、厳密な意味で要求されるものではないことに注意されたい。（不動点であるための連続性といった）求められる性質は同相写像の下で不変であるため、ブラウワーの不動点定理は、定義域が閉単位球 Dⁿ であるように要求される場合と同値な形式を持つ。同じ理由で、閉球（したがって閉、有界、連結で穴のないものなど）と位相同型であるようなすべての集合に対して定理は成り立つ。

穴を持つ定義域においてブラウワーの不動点定理が成立しない例を次に示す。極座標において定義される次の函数を考える：

${\displaystyle f(r,\theta )=(r,\theta \pi /4)}$

この函数は単位円周からそれ自身への連続函数である。この函数は、単位円周上のすべての点を反時計回りに45度回転させるものであるため、不動点を持つことはない。単位円周は閉かつ有界であるが、穴を持つ（したがって凸でない）ことに注意されたい。もしこの函数を（凸である）単位円板上で定義すれば、その原点が不動点となる。

穴を持たない定義域に対するブラウワーの不動点定理の正式な一般化は、レフシェッツの不動点定理に見られる。

注釈

この定理における連続函数は、全単射でなくてもよく、全射である必要すらない。

証明の概要

写像度を用いた証明

ブラウワーによる1911年の証明は、連続写像の写像度の概念を利用したものだった。その証明に関する近年の記述は参考文献 に見られる。

${\displaystyle K={\overline {B(0)}}}$ を、原点を中心とする ${\displaystyle \mathbb {R} ^{n}}$ 内の閉単位球とする。簡単のため、${\displaystyle f:K\to K}$ は連続的微分可能とする。ある点 ${\displaystyle p\in B(0)}$ が ${\displaystyle f}$ の正則値であるとは、${\displaystyle p}$ の原像のすべての点において ${\displaystyle f}$ のヤコビアンが非特異であることをいう。特に、逆函数定理より、${\displaystyle f}$ の原像のすべての点は（${\displaystyle K}$ の内部である）${\displaystyle B(0)}$ に属する。正則値 ${\displaystyle p\in B(0)}$ における ${\displaystyle f}$ の写像度は、${\displaystyle f}$ の下での ${\displaystyle p}$ の原像についての ${\displaystyle f}$ のヤコビ行列式の符号の和で定義される。すなわち

${\displaystyle \operatorname {deg} _{p}(f)=\sum _{x\in f^{-1}(p)}\operatorname {sign} \left(\det(Df(x))\right)}$

である。写像度とは、大雑把にいうと、p のまわりの小さな集合についての原像 f の「シート」の数である。但し、そのシートが逆向きであればマイナスをかけて数えることとする。したがってこれは、回転数の概念の高次元への一般化である。

写像度は次の「ホモトピー不変性」という性質を持つ：${\displaystyle f}$ と ${\displaystyle g}$ を二階連続的微分可能な函数とし、${\displaystyle 0\leq t\leq 1}$ に対して ${\displaystyle H_{t}(x)=tf (1-t)g}$ とする。また点 ${\displaystyle p}$ はすべての t に対して ${\displaystyle H_{t}}$ の正則値であるとする。このとき、${\displaystyle \deg _{p}f=\deg _{p}g}$ が成り立つ。

${\displaystyle K}$ の境界に不動点が存在しないなら、函数

${\displaystyle H(t,x)=x-tf(x)}$

は ${\displaystyle g(x)=x-f(x)}$ から恒等函数へのホモトピーである。恒等函数はすべての点において写像度 1 となる。特に、原点でも写像度 1 であるため、${\displaystyle g}$ もまた原点で写像度 1 となる。結果として、原像 ${\displaystyle g^{-1}(0)}$ は空とはならない。${\displaystyle g^{-1}(0)}$ の元が、すなわち元の関数 f の不動点である。

さらなる一般化のためにはより多くの概念が要求される。写像度の定義は、f の特異値にまで拡張されねばならず、したがって連続函数までの拡張となる。近年のホモロジー論の進展は、写像度の構成を簡略化し、標準的な証明となっている。

ホモロジーを用いた証明

この証明は、Dⁿ の境界が (n − 1)-球面 S^n − 1 であるという事実に基づいている。

背理法より、連続函数 f : Dⁿ → Dⁿ は不動点を持たないと仮定し、矛盾を示す。Dⁿ 内の各 x に対して、仮定より f(x) と x は異なる値なので（f が不動点を持たないとは f(x) ≠ x を意味することに注意）、f(x) を端点として x を通る唯一つの半直線を引くことが出来る。この半直線に沿って、S^n − 1 上のある点が得られるので、これを F(x) とする（図を参照）。これは、レトラクションとして知られる特別なタイプの連続函数 F : Dⁿ → S^n − 1 を定義する。すなわち、終域（この場合は S^n − 1）のすべての点がその函数の不動点となる。

直感的に、S^n − 1 の上への Dⁿ のレトラクションはあり得ないように思われる。実際、n = 1 の場合は S⁰（すなわち、閉区間 D¹ の終点）が連結ですらないため、これはあり得ない。また n = 2 の場合はこれほど明らかではないが、各々の空間の基本群を利用した基本的な議論で証明することが出来る：レトラクションは、S¹ の基本群から D² の基本群への単射群準同型を導くが、はじめの群は Z と同型である一方で二つ目の群は自明群であり、これはあり得ない。n = 2 の場合はまた、非消失ベクトル場に関する定理に基づき矛盾を示すことも出来る。

n > 2 の場合にレトラクションがあり得ないことを証明するのはさらに難しい。一つの方法として、ホモロジー群を利用する方法がある：ホモロジー H_n − 1(Dⁿ) は自明であるが、H_n − 1(S ^n − 1) は無限巡回群である。このことにより、再びレトラクションが前者から後者への単射群準同型を導くため、矛盾となる。

一般化

ブラウワーの不動点定理は、多くのより一般的な不動点定理への出発点となるものである。

無限次元への直接的な一般化、すなわち、ユークリッド空間の代わりに任意のヒルベルト空間の単位球を用いるような一般化は上手くいかない。この場合の大きな問題は、無限次元ヒルベルト空間の単位球はコンパクトでないということである。例えば、実あるいは複素の二乗加可算列のヒルベルト空間 ℓ² において、列 (x_n) を ℓ² の閉単位球から、次で定義される列 (y_n) に写す写像 f : ℓ² → ℓ² を考える：

${\displaystyle y_{0}={\sqrt {1-\|x\|_{2}^{2}}}\qquad {\text{ and }}\qquad y_{n}=x_{n-1}\quad {\text{ for }}\quad n\geq 1.}$

この写像が連続であり、値域は ℓ² の単位球に含まれることが、不動点を持たないことは容易に確かめられる。

したがって、ブラウワーの不動点定理の無限次元空間への一般化は、すべてある種のコンパクト性の仮定を含むものであり、さらにしばしば凸性の仮定も含まれる。それらの定理に関する議論は無限次元空間における不動点定理を参照されたい。

より広いクラスの空間に対する有限次元の一般化も存在する：${\displaystyle X}$ を有限個の鎖状連続体の積とすると、すべての連続函数 ${\displaystyle f:X\rightarrow X}$ は不動点を持つ。ここで鎖状連続体とは（この場合は必ずしも距離空間である必要はないが、通常は距離空間である）、すべての開被覆が、${\displaystyle U_{i}\cap U_{j}\neq \emptyset }$ と ${\displaystyle |i-j|\leq 1}$ が同値であるような有限開細分 ${\displaystyle \{U_{1},\ldots ,U_{m}\}}$ を持つようなコンパクトハウスドルフ空間のことをいう。鎖状連続体の例には、コンパクト連結線型順序空間や、実数の閉区間などが含まれる。

角谷の不動点定理は、異なる方向からブラウワーの不動点定理を一般化するものである：空間は Rⁿ のままであるが、上半連続 (多価函数)対応（集合の各点に対して、その集合の部分集合を与える函数）を考える。その集合のコンパクト性と凸性は必要となる。

レフシェッツの不動点定理は、（ほとんど）任意のコンパクト位相空間に対して適用され、不動点の存在を保証する特異ホモロジーに関する条件を与える。この条件は、Dⁿ の場合は任意の写像に対して自明に成り立つものである。

関連項目

• 不動点定理
• バナッハの不動点定理
• シャウダーの不動点定理
• レフシェッツの不動点定理
• タッカーの補題
• 角谷の不動点定理
• 位相的組合せ論
• ナッシュ均衡
• ポアンカレ＝ミランダの定理 – ブラウワーの不動点定理と等しい

脚注

参考文献

• Chow, S. N.; Mallet-Paret, J.; Yorke, J. A. (1978). “Finding zeroes of maps: Homotopy methods that are constructive with probability one”. Math. of Comp. 32: 887–899. doi:10.1090/S0025-5718-1978-0492046-9. 
• Gale, D. (1979). “The Game of Hex and Brouwer Fixed-Point Theorem”. The American Mathematical Monthly 86 (10): 818–827. doi:10.2307/2320146. JSTOR 2320146. 
• Hirsch, Morris W. (1988). Differential Topology. New York: Springer. ISBN 0-387-90148-5  (see p. 72–73 for Hirsch's proof utilizing non-existence of a differentiable retraction)
• Istrăţescu, V. I. (1981). Fixed Point Theory. Reidel. ISBN 90-277-1224-7 
• Karamardian, S., ed (1977). Fixed Points: Algorithms and Applications. Academic Press. ISBN 0-12-398050-X 
• Kellogg, R. B.; Li, T. Y.; Yorke, J. A. (1976). “A constructive proof of the Brouwer fixed point theorem and computational results”. SIAM J. Numer. Anal. 13 (4): 473–483. doi:10.1137/0713041. 
• Sobolev, V. I. (2001), “Brouwer theorem”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Brouwer_theorem 

外部リンク

• Brouwer's Fixed Point Theorem for Triangles at cut-the-knot
• Brouwer theorem, from PlanetMath with attached proof.
• Reconstructing Brouwer at MathPages
• Brouwer Fixed Point Theorem at Math Images.